Spurious Forces Can Dominate the Vorticity Budget of Ocean Gyres on the C-Grid
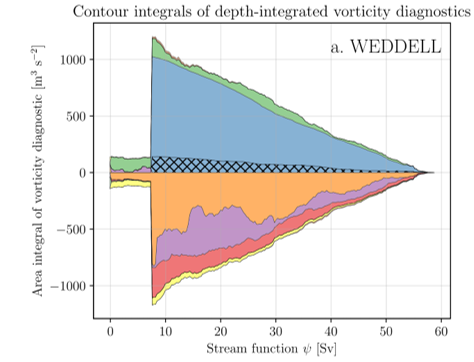 The vorticity budget of the Weddell Gyre
The vorticity budget of the Weddell Gyre
Abstract
Gyres are prominent surface structures in the global ocean circulation that often interact with the sea floor in a complex manner. Diagnostic methods, such as the depth-integrated vorticity budget, are needed to assess exactly how such model circulations interact with the bathymetry. Terms in the vorticity budget can be integrated over the area enclosed by streamlines to identify forces that spin gyres up and down. In this article we diagnose the depth-integrated vorticity budgets of both idealized gyres and the Weddell Gyre in a realistic global model. It is shown that spurious forces play a significant role in the dynamics of all gyres presented and that they are a direct consequence of the Arakawa C-grid discretization and the z-coordinate representation of the sea floor. The spurious forces include a numerical beta effect and interactions with the sea floor which originate from the discrete Coriolis force when calculated with the following schemes: the energy conserving scheme; the enstrophy conserving scheme; and the energy and enstrophy conserving scheme. Previous studies have shown that bottom pressure torques provide the main interaction between the depth-integrated flow and the sea floor. Bottom pressure torques are significant, but spurious interactions with bottom topography are similar in size. Possible methods for reducing the identified spurious topographic forces are discussed. Spurious topographic forces can be alleviated by using either a B-grid in the horizontal plane or a terrain-following vertical coordinate.